Look closely at a pinecone. Count the spirals. You'll find 8 going in one direction and 13 in the other. Look at a sunflower. You'll find 34 and 55 spirals. A pineapple? 5 and 8. These aren't random numbers. They are all part of the Fibonacci sequence, a simple mathematical pattern that seems to be the universe's favorite design template.
But what is this sequence, really? It's a kind of natural anagram. It's a rule for rearranging numbers that is echoed in the growth of plants, the shape of galaxies, and the proportions of the human body. The Fibonacci sequence and its close cousin, the Golden Ratio, are the hidden anagrams that design everything in nature.
The Universe's Favorite Anagram
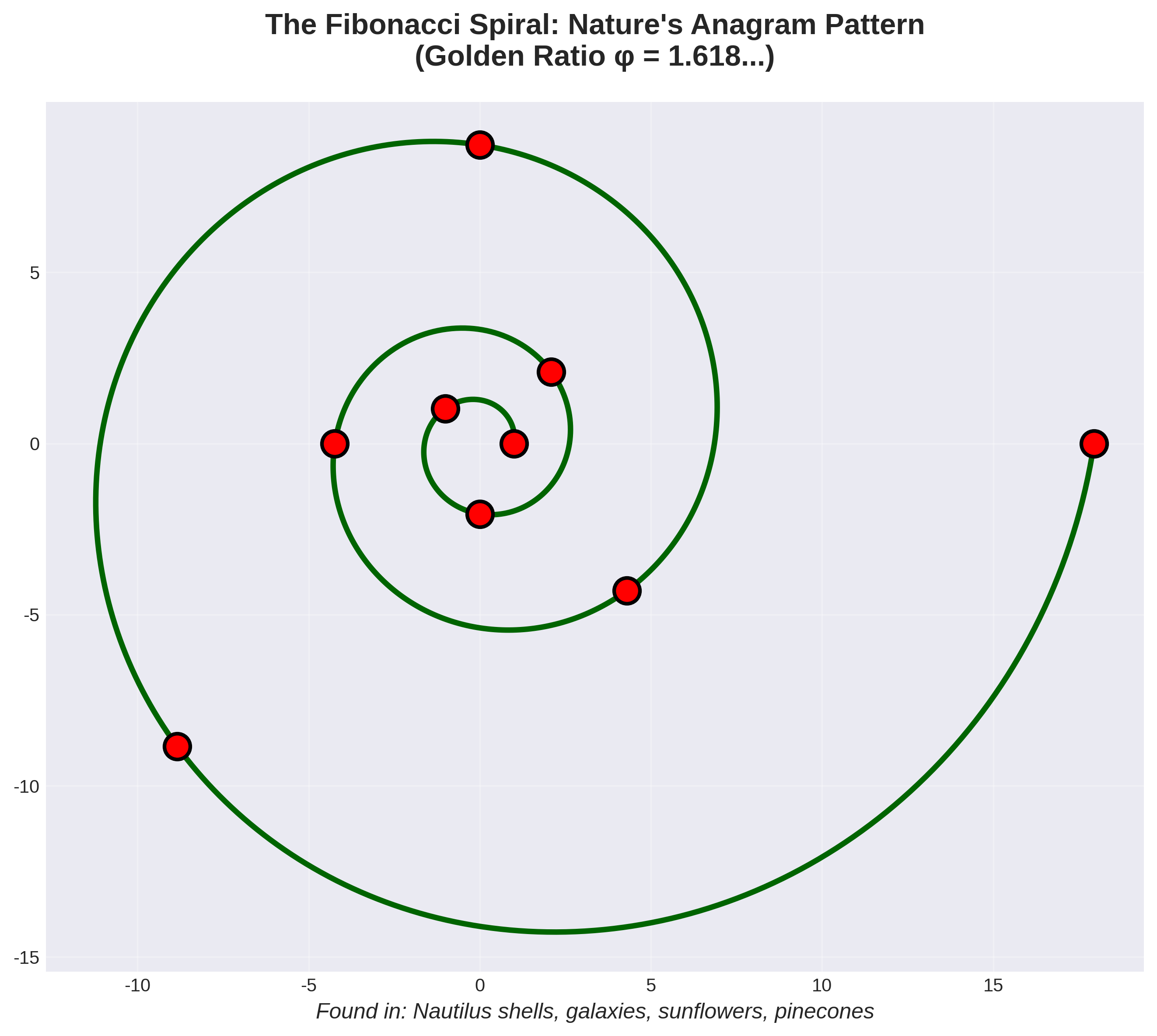
The Fibonacci sequence is deceptively simple. You start with 0 and 1, and then each subsequent number is the sum of the two preceding ones:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89...
Now, here's where the magic happens. If you take any two adjacent numbers in this sequence and divide the larger one by the smaller one, you get a number that gets closer and closer to 1.618.... This is the Golden Ratio, also known as Phi (Φ). It's been called the "divine proportion" for its prevalence in art, architecture, and, most importantly, the natural world.
Think of the Fibonacci sequence as a rule for rearranging things. It's a growth algorithm. It tells a plant how to arrange its leaves to get the most sunlight, a snail how to build its shell in a perfect spiral, and a galaxy how to form its arms.
Fibonacci in Nature
| Natural Phenomenon | Fibonacci/Golden Ratio Pattern |
|---|---|
| Flower Petals | Lilies have 3, buttercups have 5, delphiniums have 8 |
| Pinecones | 8 and 13 spirals of scales |
| Sunflower Seeds | 34 and 55 spirals |
| Nautilus Shell | A logarithmic spiral with Golden Ratio proportions |
| Spiral Galaxies | The arms follow a Fibonacci spiral |
| Human Body | Ratio of forearm to hand, face proportions |
| Tree Branching | Branches follow Fibonacci numbers |
| Hurricane Spirals | Logarithmic spiral approaching Golden Ratio |
This isn't a coincidence. It's a matter of efficiency. The Fibonacci sequence is the most efficient way to pack things together and to grow. It's nature's ultimate life hack.
Fractals: The Anagrams of Shape
The principle of rearrangement in nature goes even deeper with fractals. A fractal is a never-ending pattern that is self-similar across different scales. This means that if you zoom in on a small part of a fractal, it looks exactly like the whole thing. It's an anagram of shape.
Think of a fern. Each frond is a miniature version of the whole fern. And each leaflet on that frond is a tinier version still. This is self-similarity in action. Other examples include:
A perfect, three-dimensional fractal vegetable
Each arm has the same intricate pattern
Branching patterns repeat at every scale
Forks and branches are self-similar
Fractals are created by repeating a simple process over and over again. It's an iterative rearrangement. Just as an anagram rearranges letters to create new words, a fractal rearranges a simple shape to create infinite complexity. The study of fractals has shown that the incredible complexity we see in nature can arise from very simple rules, repeated endlessly.
The Grand Design
From the spiral of a galaxy to the petals of a flower, nature is a master anagrammatist. It takes a few simple components—numbers, shapes, physical laws—and rearranges them in an infinite variety of beautiful and complex forms.
The Fibonacci sequence and fractals are the "grammar" of this natural language. They are the rules that govern how the components can be arranged. They show us that the universe is not a random collection of stuff, but a deeply ordered and patterned system.
"The book of nature is written in the language of mathematics."
So, the next time you see a sunflower or a seashell, remember that you are looking at a solved puzzle. You are seeing the elegant solution to a mathematical problem that nature has been working on for billions of years. You are witnessing the hidden anagram pattern that designs the world.
Train your pattern recognition skills with our word puzzle tools:
Frequently Asked Questions
The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, and so on. Named after the Italian mathematician Leonardo of Pisa (known as Fibonacci), this sequence appears throughout nature in the arrangement of leaves, seeds, petals, and many other biological structures.
The Golden Ratio (Phi or φ) is approximately 1.618. It's derived from the Fibonacci sequence: when you divide any Fibonacci number by the one before it, the result approaches 1.618 as the numbers get larger. This ratio is found throughout art, architecture, and nature, and has been considered aesthetically pleasing for thousands of years.
Sunflowers (and many other plants) use Fibonacci spirals because it's the most efficient way to pack seeds. The angle between successive seeds is approximately 137.5 degrees—the Golden Angle. This prevents seeds from lining up in straight rows, maximizing the number of seeds that can fit and ensuring each gets adequate sunlight and nutrients.
Fractals are patterns that are self-similar across different scales—meaning a small part looks like the whole. Examples include ferns (each frond resembles the whole plant), romanesco broccoli, snowflakes, river deltas, and coastlines. Fractals show how complex patterns can emerge from simple rules applied repeatedly.
While the Golden Ratio does appear in various human proportions (forearm to hand, face ratios, spiral of the ear), its presence is often overstated. Many claims about the Golden Ratio in human anatomy don't hold up to rigorous measurement. However, the ratio does appear in DNA structure and other biological phenomena.
Both involve rearrangement according to rules. An anagram rearranges letters to create new words; the Fibonacci sequence is a rule for rearranging numbers to create patterns. Nature uses this mathematical 'grammar' to rearrange simple components into complex, beautiful forms—from spiral shells to branching trees.
References
- Omotehinwa, T. O., & Ramon, S. O. (2013). Fibonacci Numbers and Golden Ratio in Mathematics and Science. International Journal of Computer and Information Technology, 2(4), 633-640.
- Marples, C. R., & Williams, P. M. (2022). The golden ratio in nature: A tour across length scales. Symmetry, 14(10), 2059.
- Hutchinson, J. E. (1981). Fractals and self similarity. Indiana University Mathematics Journal, 30(5), 713-747.
- Livio, M. (2002). The Golden Ratio: The Story of Phi, the World's Most Astonishing Number. Broadway Books.